Continuous linear extension

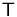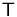In functional analysis, it is often convenient to define a linear transformation on a complete, normed vector space $X$ by first defining a linear transformation $\mathsf{T}$ on a dense subset of $X$ and then extending $\mathsf{T}$ to the whole space via the theorem below. The resulting extension remains linear and bounded (thus continuous).

This procedure is known as continuous linear extension.

1 Theorem
2 Application
3 The Hahn–Banach theorem
4 References
- 4.1 Footnotes

Theorem

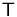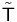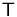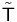Every bounded linear transformation $\mathsf{T}$ from a normed vector space $X$ to a complete, normed vector space $Y$ can be uniquely extended to a bounded linear transformation $\tilde{\mathsf{T}}$ from the completion of $X$ to $Y$ . In addition, the operator norm of $\mathsf{T}$ is $c$ iff the norm of $\tilde{\mathsf{T}}$ is $c$ .

This theorem is sometimes called the B L T theorem, where B L T stands for bounded linear transformation.

Application

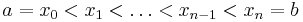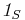Consider, for instance, the definition of the Riemann integral. A step function on a closed interval $[a,b]$ is a function of the form: $f\equiv r_1 \mathit{1}_{[a,x_1)}%2Br_2 \mathit{1}_{[x_1,x_2)} %2B \cdots %2B r_n \mathit{1}_{[x_{n-1},b]}$ where $r_1, \ldots, r_n$ are real numbers, $a=x_0<x_1<\ldots <x_{n-1}<x_n=b$ , and $\mathit{1}_S$ denotes the indicator function of the set $S$ . 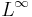The space of all step functions on $[a,b]$ , normed by the $L^\infty$ norm (see Lp space), is a normed vector space which we denote by 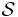$\mathcal{S}$ . 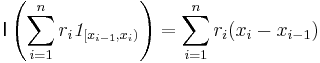Define the integral of a step function by: $\mathsf{I} \left(\sum_{i=1}^n r_i \mathit{1}_{ [x_{i-1},x_i)}\right) = \sum_{i=1}^n r_i (x_i-x_{i-1})$ . 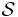$\mathsf{I}$ as a function is a bounded linear transformation from $\mathcal{S}$ into $\mathbb{R}$ .^[1]

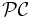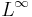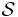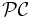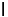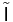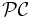Let $\mathcal{PC}$ denote the space of bounded, piecewise continuous functions on $[a,b]$ that are continuous from the right, along with the $L^\infty$ norm. The space $\mathcal{S}$ is dense in $\mathcal{PC}$ , so we can apply the B.L.T. theorem to extend the linear transformation $\mathsf{I}$ to a bounded linear transformation $\tilde{\mathsf{I}}$ from $\mathcal{PC}$ to $\mathbb{R}$ . 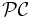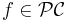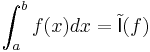This defines the Riemann integral of all functions in $\mathcal{PC}$ ; for every $f\in \mathcal{PC}$ , $\int_a^b f(x)dx=\tilde{\mathsf{I}}(f)$ .

The Hahn–Banach theorem

The above theorem can be used to extend a bounded linear transformation 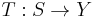$T:S\rightarrow Y$ to a bounded linear transformation from 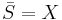$\bar{S}=X$ to $Y$ , if $S$ is dense in $X$ . If $S$ is not dense in $X$ , then the Hahn–Banach theorem may sometimes be used to show that an extension exists. However, the extension may not be unique.

References

Reed, Michael; Barry Simon (1980). Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis. San Diego: Academic Press. ISBN 0125850506.

Footnotes

^ Here, $\mathbb{R}$ is also a normed vector space; $\mathbb{R}$ is a vector space because it satisfies all of the vector space axioms and is normed by the absolute value function.